HRTEM quickstart

HRTEM quickstart#

This notebook demonstrates a basic HRTEM simulation of a double-walled carbon nanotube.

Configuration#

We start by (optionally) setting our configuration. See documentation for details.

abtem.config.set(
    {
        "device": "cpu",
        "fft": "fftw",
        "diagnostics.task_progress": True,
        "diagnostics.progress_bar": "tqdm",
    }
);

Atomic model#

In this section we create the atomic model. See our walkthough or our tutorial on atomic models.

We create two nanotubes with different radii using the nanotube function from ASE.

tube1 = ase.build.nanotube(10, 0, length=5)

tube2 = ase.build.nanotube(16, 0, length=5)

# combine the two nanotubes into a single structure
tubes = tube1 + tube2

# add vacuum in the x- and y-direction
tubes.center(vacuum=4.0, axis=(0, 1))

abtem.show_atoms(tubes, plane="xy", title="Beam view");

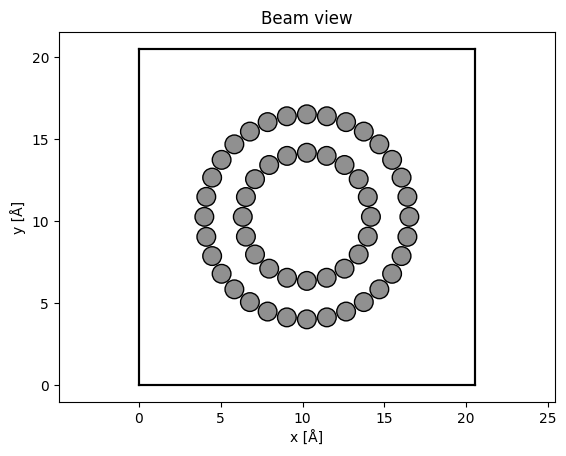
../../../_images/f4243169ceb2d2aa9cc717de58afa4cb5c8f0755636546b951898c52cdbff005.png

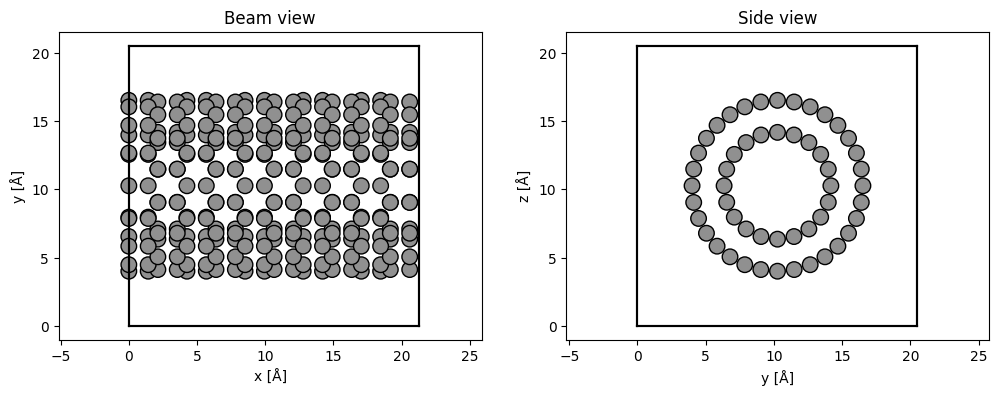
We rotate the nanotubes such the beam travels perpendicular to the length of the nanotubes.

rotated_tubes = tubes.copy()

# rotate cell and atoms by 90 degrees around y
rotated_tubes.rotate("y", 90, rotate_cell=True)

# standardize unit cell (done automatically in an abTEM simulation)
rotated_tubes = abtem.standardize_cell(rotated_tubes)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
abtem.show_atoms(rotated_tubes, plane="xy", ax=ax1, title="Beam view")
abtem.show_atoms(rotated_tubes, plane="yz", ax=ax2, title="Side view");

../../../_images/6bf44b5b637d5f63d701f1d4abb4421be08468f7927d9be1d7b1bd85552c7db9.png

Potential#

We create an ensemble of potentials using the frozen phonon model. See our walkthrough on frozen phonons.

frozen_phonons = abtem.FrozenPhonons(rotated_tubes, 32, sigmas=0.1)

We create a potential from the frozen phonons model, see walkthrough on potentials.

potential = abtem.Potential(
    frozen_phonons,
    sampling=0.05,
    projection="infinite",
    slice_thickness=1,
)

Wave function#

We create a plane wave function at an energy of 100 keV. See our walkthrough on wave functions.

wave = abtem.PlaneWave(energy=100e3)

Multislice#

We run the multislice algorithm to calculate the exit waves, see our walkthrough on multislice.

exit_wave = wave.multislice(potential)

exit_wave.compute();

Contrast transfer function#

We create a contrast transfer function of the objective lens, see our walkthrough on the contrast transfer function

Cs = -8e-6 * 1e10  # spherical aberration (-8 um)

ctf = abtem.CTF(Cs=Cs, energy=wave.energy, defocus="scherzer")

print(f"defocus = {ctf.defocus:.2f} Å")

defocus = -66.65 Å

ctf.semiangle_cutoff = ctf.crossover_angle

We include partial coherence in the quasi-coherent approximation. For more accurate descriptions of partial coherence, see our tutorial on partial coherence.

Cc = 1.0e-3 * 1e10  # chromatic aberration (1.2 mm)
energy_spread = 0.35  # standard deviation energy spread (0.35 eV)

focal_spread = Cc * energy_spread / exit_wave.energy

incoherent_ctf = ctf.copy()
incoherent_ctf.focal_spread = focal_spread

We show a profiles of the contrast transfer functions.

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
ctf.profiles().show(ax=ax1)
incoherent_ctf.profiles().show(ax=ax2, legend=True);

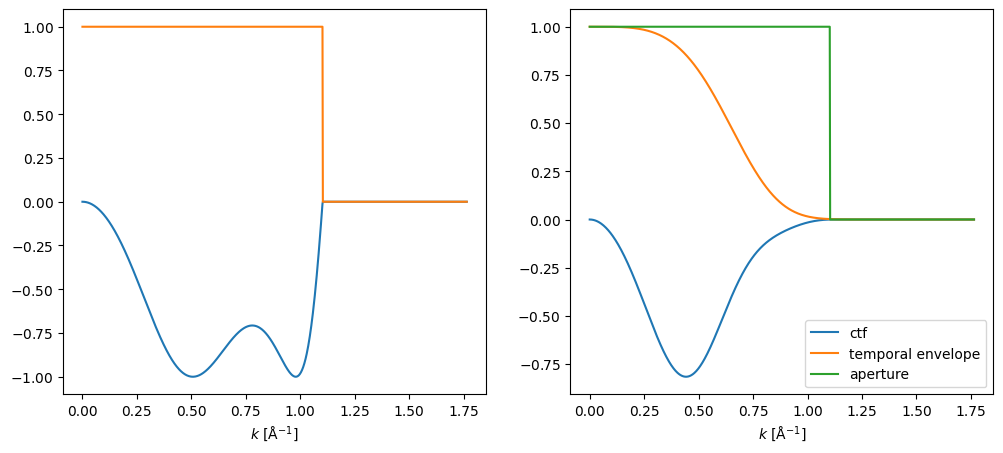
../../../_images/c37f5fe610d3679b063a47296b30e87c28ff2fa03b7d12c2eedb2683b9d940c3.png

We apply the contrast transfer function, then calculate the intensities of the wave functions.

measurement_ensemble = exit_wave.apply_ctf(incoherent_ctf).intensity()

measurement_ensemble.shape

(32, 426, 411)

The result is an ensemble of images, one for each frozen phonon, we average the ensemble to obtain the final image.

measurement = measurement_ensemble.mean(0)

measurement.show();

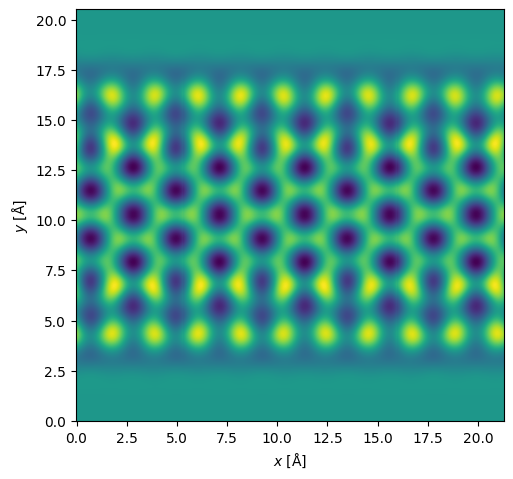
../../../_images/e2610d10c5b10cf5c15005e4e9eb7f4ea1b545f9400fef50ea9f8ddc0ccc41ed.png

Postprocessing#

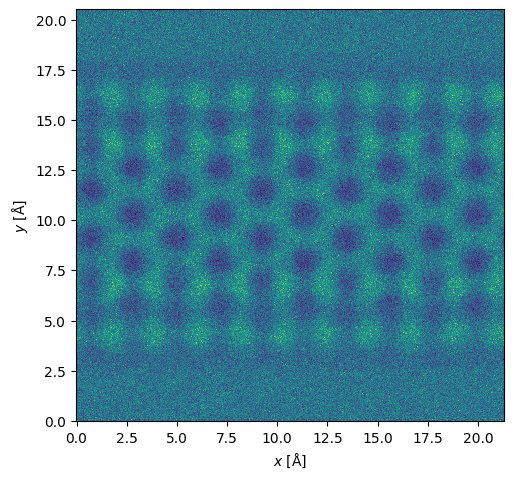
Many tasks requires additional post-processing steps. Below we apply Poisson noise to simulate the shot noise of a given finite electron dose.

noisy_measurement = measurement.poisson_noise(dose_per_area=1e4)

noisy_measurement.show()

<abtem.visualize.visualizations.Visualization at 0x1d3cff490>

../../../_images/1ea324d5e529e8b85e7be6d34a96d9b0e06add2985a21ead64054c8af8bacbf3.png

Showing the results as a line profile often provides a better sense of relative intensities.

start = (0, 0)
end = (0, potential.extent[1])

measurement.interpolate_line(start, end).show();

../../../_images/dfac87ea9392555553ae16c810aca789b4e6a00000591ec1fc3b46a05ffc833a.png